Bug with constraint equations and internal solver

Victor

Bug 25 here https://mecway.com/product.html#bugs

This could affect bolt spiders made using constraint equations but not mechanisms that couple nodes of only two elements. Whether it appears or not depends on the node numbering.

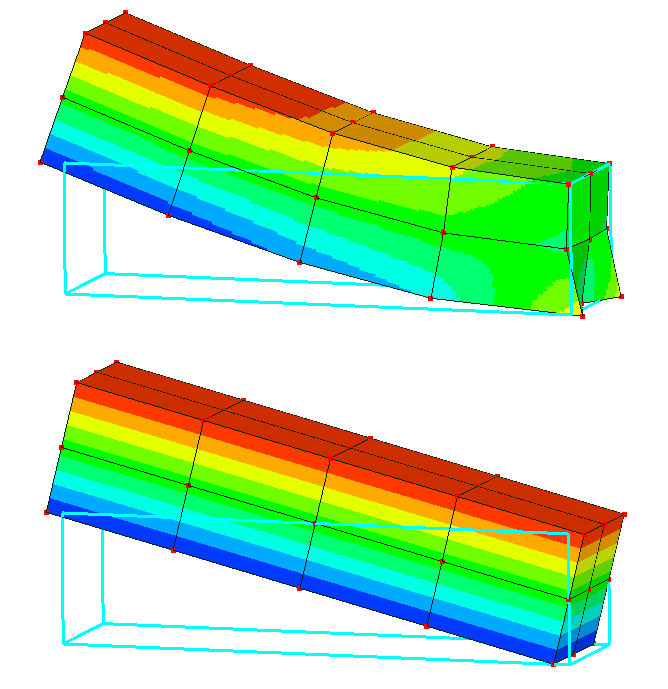
Example attached here showing a pinned support defined by equations that set the mean displacement to zero on all the nodes of a surface. One configuration has the wrong solution and the other was correctly solved by the not-yet-released Mecway version 13.

disla

Hello Victor,

I’m kind of puzzled with your bug and the liml file that has emerged it. ¿Why do you say there is a bug?
Both conditions are satisfied at the involved nodes at least with an equivalent accuracy (see pdf).
The boundary condition is kind of strange for me as it is so open that allows multiple node displacement combinations compatible with the solution.
I think the whole system is indeterminated compatible but for some reason the solver don’t warn or detect it.

If I try to solve this problem considering a force instead of a displacement in the nodes it blows up providing a nonsense solution even with ccx wich reveals there is something not properly defined in the B.C.

Victor

Yes, the equations are still satisfied, which might be why it took me so long to discover. If the nodes were not part of any elements, you'd be right that it would allow many combinations of displacements, but the stiffness of the elements is supposed to hold them together and that's not happening properly.

Since isn't only a pinned support, it should fail with a force instead of a displacement, as you found. But with a displacement BC, it's constrained against all rigid body motion. It's a truss member pinned at both ends.

disla

Hello Victor,

But if we set an infinite combination of accessible boundary conditions to a problem :

0 = 1 ux5 + 1 ux14 + 1 ux13 + 1 ux9 + 1 ux17 + 1 ux18 + 1 ux6 + 1 ux15 + 1 ux3
0 = 1 uy5 + 1 uy14 + 1 uy13 + 1 uy9 + 1 uy17 + 1 uy18 + 1 uy6 + 1 uy15 + 1 uy3

we open the door to different final stress/strain states. There is not a unique solution. I think that’s why when I impose the force to the nodes it doesn’t work. The problem is not properly constrained.
Maybe you missed to impose the symmetry on the displaced face to reflect the truss is pined in both sides.

“Since isn't only a pinned support, it should fail with a force instead of a displacement, as you found. “

I don’t think these equation model a pinned support.

0 = 1 ux5 + 1 ux14 + 1 ux13 + 1 ux9 + 1 ux17 + 1 ux18 + 1 ux6 + 1 ux15 + 1 ux3
0 = 1 uy5 + 1 uy14 + 1 uy13 + 1 uy9 + 1 uy17 + 1 uy18 + 1 uy6 + 1 uy15 + 1 uy3

¿Have you cansider that maybe you have set an unreachable equilibrium state?
If I remove this condition to something closer to a pin support and impose symetry the problem can be solved both with displacement , with force and with both ccx and internal exactly with the same results.
I would ask , ¿Is your solution compatible with the BC? We found it is. Maybe not the expected solution but not a bug.

Thanks for your patience.

Victor

The equations mean "average displacement = 0" in the X and Y directions, so there must be no overall motion of that group of nodes in the XY plane, which you've confirmed with your spreadsheet. There can be rotation and stretching of the whole group though, so it's a kind of distributed pinned support, not a concentrated one like in your example.

The "bug" solution still satisfies the boundary conditions so in that sense it's correct. The problem is not that the BCs are violated but that some parts of the adjacent elements aren't fully connected to those nodes so they get pulled in strange directions without their stiffness to keep them close to their original shapes.

You can solve it in CCX and see that it behaves like a truss member with no bending.

I didn't intend to use symmetry, but the problem is still there in the middle case of your updated model with symmetry so it's not because it's underconstrained.